백준[BOJ] 1707번 : 이분그래프 - BFS, DFS
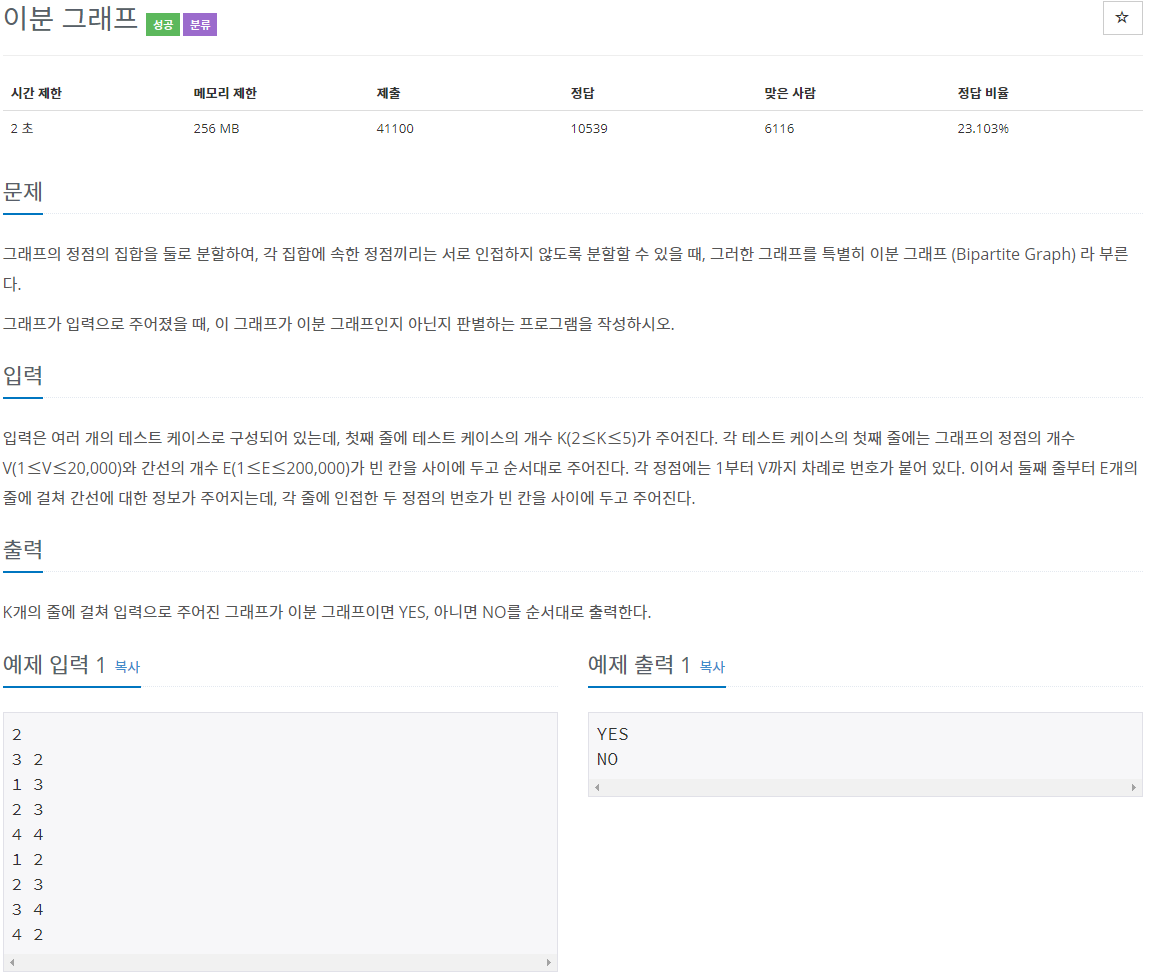
1707번: 이분 그래프
입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K(2≤K≤5)가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V(1≤V≤20,000)와 간선의 개수
www.acmicpc.net
BFS, DFS를 연습하기 좋은 문제라는 생각이 든다.
처음에 이분 그래프의 개념을 아예 몰라서, 이진트리를 의미하는 줄 알고 한참 고생했다....
그림으로 보면 이해가 빠르다. 아래와 같다. 인접한 정점을 다른 색으로 모두 칠할 수 있으면 이분 그래프이다.

이분 그래프의 특징
- 인접한 정점들을 다른 색을 구분할 수 있다.
- 순환할 수 있다.(2가지 색으로 구분 가능하면 된다.)
- 최대 이분 매칭 문제(Maximum Bipartite Matching Problem, MBP), 최대 유량 문제(Maximum Flow Problem) 등에 활용할 수 있다.
- 공부할 영역이 더 많은 부분이라, 확실하게 알고 넘어가야한다!!
문제 풀 때 유의사항
- 모든 연결 요소(Connected Component)를 확인해야한다. => 모든 정점을 방문했는지 확인 필수!
- 정점의 최대 개수(V)가 2만개, 최대 간선(E) 20만개. =>인접행렬 O(V^2) >>인접리스트 O(E) 사용
- 간선을 따라 이동하면서, 모든 정점을 확인한다. 간선의 개수 E와 정점의 개수 V에 대하여 시간 복잡도는 O( V+E )이다.
- 모든 정점을 방문하는 과정에서 인접한 두 정점만 비교하면 되므로, DFS(반복, 재귀)와 BFS 모두 가능하다.
DFS 반복 / DFS 재귀 / BFS 반복 3가지 버전을 모두 구현해보고 결과를 비교해보았다!
첫 번째
- BFS ( 너비우선탐색 ) -
- 필요한 변수 -
- 탐색에 필요한 queue<int node, bool type>
- 간선 리스트를 작성할 2차원 배열. (vector<vector<int>> list)
- 정점의 상태를 나타낼 1차원 배열 (vector<int> visit / 0 : 방문안함 / 1, -1 : 정점의 구분, 색칠하기)
- BFS 함수 -
[ INPUT ]
- int start : 탐색을 시작할 노드 번호
- vector<int>& visit : 전체 노드의 상태 ( '0' - 미방문 / '1'- true / '-1' - false )
- vector<vector<int>> list : 탐색할 그래프의 간선리스트
[ OUTPUT ] : NONE
[ RETURN ]
- bool : 탐색한 그래프가 이분그래프이면 true / 탐색 중 인접한 노드가 같은 색이면 false를 반환
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
bool bfs(int, vector<int>&, vector<vector<int>>&);
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
vector<int> visit;
vector<vector<int>> list;
int k, v, e, v1, v2;
cin >> k;
while (k--) {
cin >> v >> e;
// initializing in every testCase
visit.clear(); visit.resize(v + 1);
list.clear(); list.resize(v + 1);
// constucting egde list
for (int i = 0; i < e; i++) {
cin >> v1 >> v2;
list[v1].push_back(v2);
list[v2].push_back(v1);
}
// make start-point
int start;
for(int i = 1; i<= v; i++)
if (list[i].size() > 0) {
start = i;
break;
}
// do
if (bfs(start, visit, list))
cout << "YES\n";
else
cout << "NO\n";
}
}
bool bfs(int start, vector<int>& visit, vector<vector<int>>& list) {
// pair<nodeNumber, colorType>
// colorType : T or F - colorType
queue<pair<int, bool>> q;
q.push(make_pair(start, true));
while (!q.empty()) {
int node = q.front().first;
bool type = q.front().second;
q.pop();
visit[node] = (type ? 1 : -1);
for (int i = 0; i < list[node].size(); i++) {
int nextNode = list[node][i];
// already visited before!!
if (visit[nextNode] != 0) {
// Terminal Case
if (visit[node] == visit[nextNode])
return false;
else
continue;
}
else
q.push(make_pair(nextNode, !type));
}
// check the other Connected-Components
if (q.empty())
for (int i = 1; i < visit.size(); i++)
if (!visit[i]) {
q.push(make_pair(i, true));
break;
}
}
return true;
}
- 실행결과 -

두 번째
- DFS ( 깊이우선탐색 ) ver.반복 -
- 필요한 변수 -
- 탐색에 필요한 stack<int node, bool type>
- 간선 리스트를 작성할 2차원 배열. (vector<vector<int>> list)
- 정점의 상태를 나타낼 1차원 배열 (vector<int> visit / 0 : 방문안함 / 1, -1 : 정점의 구분, 색칠하기)
- DFS 함수 -
[ INPUT ]
- int start : 탐색을 시작할 노드 번호
- vector<int>& visit : 전체 노드의 상태 ( '0' - 미방문 / '1'- true / '-1' - false )
- vector<vector<int>> list : 탐색할 그래프의 간선리스트
[ OUTPUT ] : NONE
[ RETURN ]
- bool : 탐색한 그래프가 이분그래프이면 true / 탐색 중 인접한 노드가 같은 색이면 false를 반환
#include <iostream>
#include <stack>
#include <vector>
using namespace std;
bool dfs(int, vector<int>&, vector<vector<int>>&);
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
vector<int> visit;
vector<vector<int>> list;
int k, v, e, v1, v2;
cin >> k;
while (k--) {
cin >> v >> e;
// initializing in every testCase
visit.clear(); visit.resize(v + 1);
list.clear(); list.resize(v + 1);
// constucting egde list
for (int i = 0; i < e; i++) {
cin >> v1 >> v2;
list[v1].push_back(v2);
list[v2].push_back(v1);
}
// make start-point
int start;
for(int i = 1; i<= v; i++)
if (list[i].size() > 0) {
start = i;
break;
}
// do
if (dfs(start, visit, list))
cout << "YES\n";
else
cout << "NO\n";
}
}
bool dfs(int start, vector<int>& visit, vector<vector<int>>& list) {
// pair<nodeNumber, colorType>
// colorType : T or F - colorType
stack <pair<int, bool>> s;
s.push(make_pair(start, true));
while (!s.empty()) {
int node = s.top().first;
bool type = s.top().second;
s.pop();
visit[node] = (type ? 1 : -1);
for (int i = 0; i < list[node].size(); i++) {
int nextNode = list[node][i];
// already visited before!!
if (visit[nextNode] != 0) {
// Terminal Case
if (visit[node] == visit[nextNode])
return false;
else
continue;
}
else {
s.push(make_pair(node, type));
s.push(make_pair(nextNode, !type));
break;
}
}
// check the other Connected-Component
if (s.empty())
for (int i = 1; i < visit.size(); i++)
if (!visit[i]) {
s.push(make_pair(i, true));
break;
}
}
return true;
}
- 실행결과 -

세 번째
- DFS ( 깊이우선탐색 ) ver.재귀 -
- 필요한 변수 -
- 탐색에 필요한 stack<int node, bool type>
- 간선 리스트를 작성할 2차원 배열. (vector<vector<int>> list)
- 정점의 상태를 나타낼 1차원 배열 (vector<int> visit / 0 : 방문안함 / 1, -1 : 정점의 구분, 색칠하기)
- DFS_recursive 함수 -
[ INPUT ]
- int start : 탐색을 시작할 노드 번호
- bool type : 색깔. ( true 면 visit에 1로 저장 / false 면 visit에 -1로 저장 )
- vector<int>& visit : 전체 노드의 상태 ( '0' - 미방문 / '1'- true / '-1' - false )
- vector<vector<int>> list : 탐색할 그래프의 간선리스트
[ OUTPUT ] : NONE
[ RETURN ]
- bool : 탐색한 그래프가 이분그래프이면 true / 탐색 중 인접한 노드가 같은 색이면 false를 반환
#include <iostream>
#include <stack>
#include <vector>
using namespace std;
bool dfs_re(int, bool, vector<int>&, vector<vector<int>>&);
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
vector<int> visit;
vector<vector<int>> list;
int k, v, e, v1, v2;
cin >> k;
while (k--) {
cin >> v >> e;
// initializing in every testCase
visit.clear(); visit.resize(v + 1);
list.clear(); list.resize(v + 1);
// constucting egde list
for (int i = 0; i < e; i++) {
cin >> v1 >> v2;
list[v1].push_back(v2);
list[v2].push_back(v1);
}
// do
bool success = true;
for (int i = 1; i < visit.size(); i++) {
if (!visit[i]) {
success = dfs_re(i, true, visit, list);
if(!success) break;
}
}
if (success) cout << "YES\n";
else cout << "NO\n";
}
}
bool dfs_re(int node, bool type, vector<int>& visit, vector<vector<int>>& list) {
int success = true;
visit[node] = (type ? 1 : -1);
for (int i = 0; i < list[node].size(); i++) {
int nextNode = list[node][i];
// already visited before!!
if (visit[nextNode] != 0) {
// terminal case
if (visit[node] == visit[nextNode])
return false;
else
continue;
}
else
success = dfs_re(nextNode, !type, visit, list);
}
return success;
}
- 실행결과 -

- 결과 비교 -
| 메모리 | 시간 | |
| BFS | 11464 KB | 280 MS |
| DFS - 반복 | 6296 KB | 524 MS |
| DFS - 재귀 | 6480 KB | 260 MS |
: 메모리나 시간 측면에서 재귀적으로 구현한 DFS가 가장 성능이 좋았다.
: (해당 테스트 케이스를 직접 보아야 알겠지만) 수치로만 보자면 BFS가 DFS의 2배의 메모리를 사용하는 것을 알 수 있다. BFS는 같은 깊이에 있는 모든 정점을 큐에 넣게 되고, DFS는 한번에 내려갈 수 있는 최대 깊이까지만 내려간다. 테스트 케이스에 있는 그래프가 세로보다는 가로로 더 길기 때문인가? BFS의 메모리가 더 적게 나오려면 자식 노드가 하나씩 길게 내려가야 한다. 그렇게 되면 그래프로서의 기능이 최소화된다. 이진트리의 경우를 따져보자 높이는 log2N / 한 층의 최대 너비는 2N 이다. 공간복잡도는 logN : N 의 비율이 나올것이다. 평균적인 그래프의 모양이 깊어질수록 넓어지기 때문인듯하다.
: 시간은 BFS와 DFS(재귀) 가 비슷한 시간을 보여주고 있다. 모든 정점을 간선을 통해 탐색하기 때문에 시간 복잡도는 O ( V + E ) 로 동일하다. 흥미로운 점은 반복적 DFS가 2배 정도 시간이 더 걸린 것이다. 보통은 재귀함수로 구현했을 때가 시간이 더 걸린다. 이 때문에 세 버전의 코드 간 차이점을 살펴보았다. 유의미한 차이는 한번도 방문하지 않은 정점을 마주했을 때의 코드이다.( BFS - 78번째 줄 / DFS 반복 -78번째 줄 / DFS 재귀 - 64번째 줄) 나머지 부분에서의 연산 횟수는 동일하지만 이곳에서만 차이가 있다. BFS와 DFS재귀에서는 연산 회수가 1번인데 반해, 반복DFS 일 때만 해당 코드에서 pair 객체를 2번 만들어낸다. DFS 재귀보다 BFS가 조금 더 느린 이유도, BFS는 pair 객체를 생성한 후 복사하여 넘겨주는 반면에, DFS재귀는 재귀함수를 호출하기 때문인듯하다.
위와 같은 결론을 얻기는 했지만, 단순히 추론이기 때문에 더 정확한 분석과 근거가 있었으면 좋겠다.